Gracias chic@s por vuestro trabajo y no bajéis la guardia pese a las circunstancias. Hoy os planteo tres ejercicios, como siempre después pondré las soluciones pero recordad que es importante intentarlo porque sabéis, sois inteligentes, podéis ... y tener siempre presente que "toda dificultad es una superación de vosotros mismos"
Ejercicio 1
Dada la recta de ecuación 2x-3y+6=0, escríbela en forma contínua, paramétrica, vectorial y explícita.
Ejercicio 2
El punto P (3,1), ¿pertenece a la recta que pasa por el punto A (-2,-2) y tiene como vector director v=(1,3)?
Ejercicio 3
Determina la ecuación de las rectas siguientes y expresa en forma implícita y explicita:
a: la recta que corta los ejes de coordenadas en los puntos C(0,-1) D(3,0)
b: la recta que pasa por el punto A(1,-2) y tiene pendiente m=-2
SOLUCIONES
SOL 1
Dada la recta de ecuación 2x-3y+6=0, escríbela en forma contínua, paramétrica, vectorial y explícita.
Tenemos la siguiente recta:
Necesitamos obtener el vector de dirección y un punto que pertenece a la recta. Con estos dos datos, podemos obtener la ecuación vectorial, la paramétrica y la contínua.
Cuando la recta está en forma genera Ax+By+C=0 el vector director es v(-B, A). Entonces en nuestrocaso el vector de dirección es:
Para obtener un punto de la recta, le damos a x el valor que queramos, por ejemplo x=0 y despejamos el valor de «y»:
Por lo que el punto que pertenece a la recta es:
Con este punto y el vector de dirección obtenemos la ecuación vectorial:

Y la ecuación contínua:
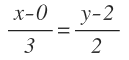
La ecuación explícita la vamos a obtener a partir de la general
despejando la "y", entonces
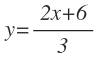
Finalmente, separamos la fracción en dos términos para que se quede en forma explícita:

Sol 2
El punto P (3,1), ¿pertenece a la recta que pasa por el punto A (-2,-2) y tiene como vector director v=(1,3)?
Para saber si el punto pertenece a la recta, vamos a calcular la ecuación contínua y después sustituiremos las coordenadas del punto por la x y por la «y» en la recta y veremos si se cumple al igualdad.
Entonces, tenemos el punto y el vector de dirección:
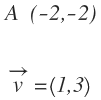
En la ecuación contínua:
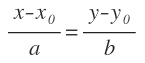
Sustituimos X0 e Y0 por las coordenadas del punto, y a y b por las coordenadas del vector de dirección:
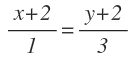
Ya tenemos la ecuación contínua.
Ahora, vamos a ver si el punto P (3,1) pertenece a esa recta, y para eso tiene que cumplir la ecuación:
Sustituimos sus coordenadas por x y por «y»:

Operamos en ambos miembros y vemos que no se cumple la igualdad:
Por tanto, el punto P (3,1) no pertenece a la recta
Sol 3
Determina la ecuación de las rectas siguientes y expresa en forma implícita y explicita:
a: la recta que corta los ejes de coordenadas en los puntos C(0,-1) D(3,0)
Tenemos los puntos:
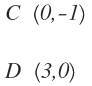
Necesitamos un punto y un vector. Como punto nos vale cualquiera de los dos por ejemplo C(0, -1) y como vector el CD=D-C=(3, 1). Entonces hallamos la ecuación continua:

Para obtener la ecuación implícta multiplicamos en cruz y pasamos todos los términos para un lado de la igualdad:
Para obtener la ecuación explícita, despejamos la «y»:

Y separamos en dos términos, uno con x y otro sin x:
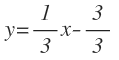
Y simplificamos el segundo término:
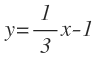
b: la recta que pasa por el punto A(1,-2) y tiene pendiente m=-2
Tenemos un punto y la pendiente:
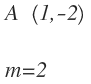
Calcularemos la ecuación de la recta con la ecuación punto pendiente:
Sustituimos X0 e Y0 por las coordenadas del punto y m por su valor:
Operamos:
La ecuación implícita la obtenemos pasando todos los términos al primer miembro y reordenando:
Y la ecuación explícita despejando «y»:
No hay comentarios:
Publicar un comentario
Si tenéis dudas también podéis comunicármelas a través de comentarios en la entrada.