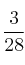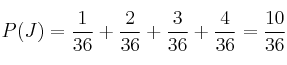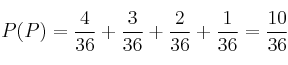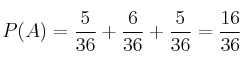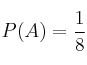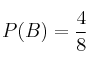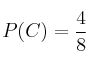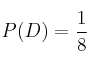sábado, 1 de enero de 2050

PRESENTACIÓN
Hola chic@s, gracias por conectaros, espero que durante estos días podamos hacer un repaso de lo ya aprendido y avanzar un poco en la asignatura, esperando que todo vuelva a la normalidad lo más pronto posible.
Para cualquier duda podéis enviarme un mensaje al siguiente dirección de email: direccionpondal@gmail.com

Cada entrada del blog se corresponde con la tarea planteada para cada día que en vuestro horario tuvieseis matemáticas y mientras dure el aislamiento iré colgando más tareas, por lo que tendréis que visitar el blog periódicamente. Las actividades planteadas tendréis que realizarlas en el cuaderno de clase así que mucho ánimo.

Aquí os dejo una interesante conferencia de un gran comunicador llamado Eduardo Sáenz para aquellos que queráis visualizarla. Trata sobre las matemáticas y la educación que espero que os haga reflexionar.

By en No hay comentarios:

domingo, 9 de agosto de 2020

 

Hola chicos, es hora de poneros ya más en serio a repasar para el curso que viene.

Adjunto el siguiente link:

 https://www.matematicasonline.es/BachilleratoCCNN/Primero/mat1-Bach-ciencias8.htmlen

En el  encontraréis ejercicios de repaso para que podáis prepararos. Como veréis hay muchas partes que ya vimos este año en 4º ESO   y que recomiendo que hagáis para repasar como son Números reales, intervalos, potencias y raíces, Expresiones algebráicas. Polinomios, Ecuaciones e Inecuaciones, Sistemas de ecuaciones. Método de Gauss, Trigonometría o vectores y rectas. Estas son las partes que necesitáis repasar y al nivel que vimos este curso. Que nadie se agobie si no le sale  algún  ejercicio. Yo estoy disponible en el mail para resolveros cualquier duda.

Después hay partes que las dareis nuevas en bahillerato y que ya os explicarán. Me parece además que es una web interesante que además os puede servir de ayuda de cara al curso que viene.

Mucho ánimo.




By en No hay comentarios:

jueves, 2 de julio de 2020

03 Julio 2020



Hola chic@s, vamos a seguir repasando para prepararnos para bachillerato. Es muy importante tener dominadas ciertas herramientas de cálculo porque el año que viene vais a encontraros con conceptos nuevos pero necesitareis dominar el cálculo numérico, las ecuaciones, polinomios, etc para poder abordar la nueva materia. No se trata de que os agobiéis, simplemente de que reforcéis algunas cosas de este curso. Os iré poniendo ejercicios para que repaséis y estaré pendiente del mail para ayudaros en todo lo que pueda. Recordad que en matemáticas se saben las cosas cuando se entienden así que cualquier duda por pequeña que sea me la preguntáis porque estaré encantado de responderos.

Os pongo ejercicios de repaso de la primera evaluación. Tener en cuenta que primero deberéis de tener clara la teoría y para eso podéis consultar vuestro libro de texto y además os dejo unos links donde aparece teoría acompañada de ejercicios que os puede ayudar en caso de duda:









By en No hay comentarios:

martes, 16 de junio de 2020

16 JUNIO 2020



Bueno a partir de ahora voy a proponer una serie de actividades de repaso de todo el curso para aquellos que vayáis a hacer un bachillerato en el que tengáis la asignatura de matemáticas. Como siempre estaré disponible en el mail direccionpondal@gmail.com para atender a vuestras dudas.

Hoy os propongo una prueba para repasar conceptos de la 1ª Evaluación:






By en No hay comentarios:

miércoles, 10 de junio de 2020

10 y 12 JUNIO 2020


Hola chic@s, os dejo los últimos ejercicios de probabilidad para que hagáis. Aquí finalizaremos la materia de este curso, a partir de hoy empezaremos a hacer un repaso de todo el curso. A todos aquellos que halláis decidido hacer un bachillerato en el que tengáis la asignatura de matemáticas os recomiendo que realicéis las tareas que os proponga porque el curso que viene lo agradeceréis, sería un error pensar que el año que viene tenéis tiempo suficiente para poneros al día y por lo tanto no es cuestión de agobiarse sino de ir haciendo tareas de repaso poco a poco. Trataré de poneros ejercicios con soluciones y estaré disponible en el mail para aquellos que lo necesitéis.

Ejercicios de probabilidad: 


1. Lanzamos dos dados y anotamos la suma de puntos de ambos dados.
Juan gana si la suma de puntos es 5 o menos
Pedro gana si la suma de puntos es 9 o más
Antonio gana si la suma de puntos es 6, 7 u 8
¿Quién tiene más probabilidad de ganar?

SOLUCIÓN

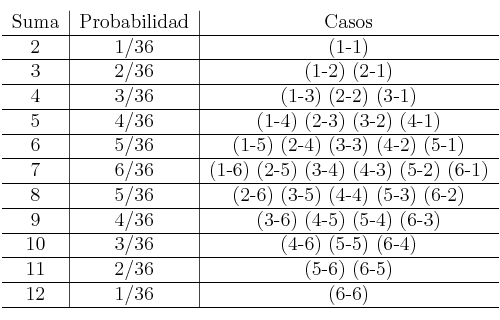
1. Al sumar los puntos de dos datos obtendremos unos valores que oscilan entre 2 (1+1) y 12 (6+6).
Además debemos recordar que el nº de casos posibles es 6 x 6 = 36
Expresamos esos datos en una tabla
\begin{tabular}{c|c|c} Suma & Probabilidad & Casos\\ \hline 2 & 1/36 & (1-1)\\ \hline 3 & 2/36 & (1-2) (2-1)\\ \hline 4 & 3/36 & (1-3) (2-2) (3-1) \\ \hline 5 & 4/36 & (1-4) (2-3) (3-2) (4-1)\\ \hline 6 & 5/36 & (1-5) (2-4) (3-3) (4-2) (5-1)\\ \hline 7 & 6/36 & (1-6) (2-5) (3-4) (4-3) (5-2) (6-1)\\ \hline 8 & 5/36 & (2-6) (3-5) (4-4) (5-3) (6-2)\\ \hline 9 & 4/36 & (3-6) (4-5) (5-4) (6-3) \\ \hline 10 & 3/36 & (4-6) (5-5) (6-4)\\ \hline 11 & 2/36 & (5-6) (6-5)\\ \hline 12 & 1/36 & (6-6)\\ \hline \end{tabular}
Sean los sucesos:
J = "gana Juan"
P = "gana Pedro"
A = "gana Antonio"
Entonces las probabilidades son:
- P(J) = \frac{1}{36}+\frac{2}{36}+\frac{3}{36}+\frac{4}{36}=\frac{10}{36}
- P(P) = \frac{4}{36}+\frac{3}{36}+\frac{2}{36}+\frac{1}{36}=\frac{10}{36}
- P(A) = \frac{5}{36}+\frac{6}{36}+\frac{5}{36}=\frac{16}{36}
Antonio tiene más probabilidad de ganar

2. Lanzamos tres monedas. Se pide:
- a) probabilidad de obtener tres caras
- b) probabilidad de obtener al menos dos caras
- c) probabilidad de obtener como mucho una cara
- d) probabilidad de no obtener ninguna cara

SOLUCIÓN

Al lanzar tres monedas obtenemos el siguiente Espacio Muestral compuesto por 8 sucesos elementales:
E = \{CCC, \quad CC+, \quad C+C, \quad C++, \quad +CC, \quad +C+, \quad ++C, \quad+++ \}
Sean los sucesos:
- A = "obtener tres caras"
- B = "obtener al menos dos caras"
- C = "obtener como mucho una cara"
- D = "no obtener ninguna cara"
Entonces las probabilidades serían:
- P(A) = \frac{1}{8}
- P(B) = \frac{4}{8}
- P(C) = \frac{4}{8}
- P(D) = \frac{1}{8}

3. Lanzamos tres monedas. Se pide:
- a) probabilidad de obtener tres caras
- b) probabilidad de obtener al menos dos caras
- c) probabilidad de obtener como mucho una cara
- d) probabilidad de no obtener ninguna cara

SOLUCIÓN

Al lanzar tres monedas obtenemos el siguiente Espacio Muestral compuesto por 8 sucesos elementales:
E = \{CCC, \quad CC+, \quad C+C, \quad C++, \quad +CC, \quad +C+, \quad ++C, \quad+++ \}
 Sean los sucesos:
- A = "obtener tres caras"
- B = "obtener al menos dos caras"
- C = "obtener como mucho una cara"
- D = "no obtener ninguna cara"
Entonces las probabilidades serían:
- P(A) = \frac{1}{8}
- P(B) = \frac{4}{8}
- P(C) = \frac{4}{8}
- P(D) = \frac{1}{8}
4. Elegimos al azar una ficha de un juego de dominó. Calcula la probabilidad de:
- a) obtener el pito doble (1-1)
- b) la suma de puntos sea 7

SOLUCIÓN

Un dominó consta de 28 fichas numeradas como en la imagen
- a) \frac{1}{28}
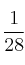
- b) Para que la suma de puntos sea 7 tenemos estas posibilidades:
[1-6] [2-5] y [3-4]
\frac{3}{28}

By en No hay comentarios:
Suscribirse a: Entradas (Atom)
  • 10 y 12 JUNIO 2020
    Hola chic@s, os dejo los últimos ejercicios de probabilidad para que hagáis. Aquí finalizaremos la materia de este curso, a partir de hoy ...
  • (sin título)
      Hola chicos, es hora de poneros ya más en serio a repasar para el curso que viene. Adjunto el siguiente link:   https://www.matematicasonl...
  • 25 MAYO 2020
    Buenos días chic@s, hoy vamos a ver el domino de las funciones LOGARÍTMICAS. Recordamos que solamente se pueden hallar logaritmos d...